Astrofotografie :: Die optische Projektion

Die optische Projektion

Wie groß ist der Vollmond von der Erde aus gesehen? Rund 32 Bogenminuten sagen die Astronomen, aber wieviel Millimeter sind das? Denn auf dem Papierabzug einer Aufnahme oder seiner Abbildung auf dem Bildschirm gibt es keine Bogenminuten, sondern nur Millimeter und Bildpunkte! Betrachtet man nun den Vollmond auf dem Bildschirm, taucht recht schnell die Frage auf "der wievielfachen Vergrößerung entspricht das?". Zur korrekten Beantwortung dieser Frage muß man zwei Dinge streng voneinander trennen - das Objekt selbst und die Abbildung - Projektion - dessen auf eine Fläche, egal ob auf ein Stück Papier, auf einen Kamerachip oder auf eine Bildschirmoberfläche.

Betrachten wir zum Einstieg in dieses verzwickte Thema mal den Vollmond am Nachthimmel. Eine große Kugel - möchten wir meinen. Doch hier lassen wir uns ganz böse täuschen!

Was sehen wir wirklich? Ein kleines Kügelchen, das gerade mal den 16-fachen Durchmesser dessen hat, was wir so gerade noch als Kügelchen und nicht als Punkt wahrnehmen können. Betrachten wir mal die beiden (identischen!!!) Bilder oben aus einer Entfernung von ca. 1,2m, dann sehen wir den Vollmond in der korrekten Größe!

Dazu eine ungewöhnliche Frage: Welches Objekt erscheint uns größer - der Vollmond am Nachthimmel oder eine CD aus 13m Entfernung betrachtet? Die Antwort wird die meisten verwundern: Beide Objekte erscheinen uns gleich groß!

Aber es kommt noch besser: Was wir letztendlich sehen, ist nicht der Vollmond selbst, sondern "nur" dessen Projektion durch unsere Augenlinse auf unsere Netzhaut. Maßgebend ist dann allerdings das, was unser Gehirn aus diesen Informationen macht - einen viel zu großen Vollmond am Nachthimmel zum Beispiel.

Wie wird nun aus einer Bogenminute (') ein Millimeter? Die folgende - optisch freilich nicht ganz korrekte Skizze - soll dies an einem Beispiel verdeutlichen:

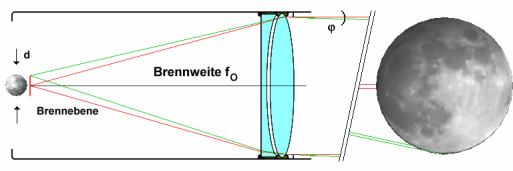
Das Licht vom Vollmond erreicht das Objektiv des Refraktors in einem Winkel von φ=16', das heißt, daß die an sich parallelen Lichtstrahlen von einem Punkt in der Mondmitte und von einem am unteren Mondrand das Objektiv in einem Winkel von 16' erreichen. Damit erscheint uns der "komplette" Vollmond in einem Winkel von 2×16'=32'. Das Objektiv mit der Brennweite von f_O bildet beide Punkte in der Brennebene wieder punktförmig ab, wobei diese beiden Punkte dort einen Abstand von d/2 haben. Nun ist es also passiert - aus ein paar Bogenminuten sind ein paar Millimeter geworden - wir haben eine Projektion!

Mit ein wenig einfacher Mathematik können wir nun den Abstand dieser Punkte bestimmen:

d/2=f_O×tan(φ)
oder
d=2×f_O×tan(φ)

Setzen wir mal ein paar Zahlenwerte ein, sagen wir f_O=1.500mm, dann haben wir

d/2=1.500mm×tan(16')=7mm

Unser Vollmond hat in der Brennebene des Refraktors also einen Durchmesser von 14mm.

Bei der Frage nach der Vergößerung müssen wir das "Auflösungsvermögen" unserer Augen berücksichtigen. Am Nachthimmel können wir 2' (=120") so gerade noch auflösen, während wir auf dem Papier Strukturen von 0,1 mm (aus 20 cm Entfernung) so eben noch erkennen können. Wenn wir das also mal gleichsetzen, also 2' ≡ 0,1 mm, dann hätten wir in diesem Beispiel eine Vergrößerung V_P von:

V_P=7mm/16' × 2'/0,1mm = 140/16 = 8,75

Das ist nicht besonders viel, aber für ein paar Krater reicht es aus.

Nun wird es ein wenig komplizierter: Wir bringen einen Kamerachip in die Brennebene. Dieser besteht aus Millionen winzig kleiner, lichtempfindlicher Zellen, die auf ihm wie auf einem Schachbrett angeordnet sind. Der Abstand P_w zwischen jeweils 2 Zellen beträgt im allgemeinen so um die 6μm (=0,006mm). Unser Mond in der Brennebene wird also
 

P_B = d/P_w = 2.333 für P_w = 6μm

Betrachtet man diesen Bildschirm nun aus einer Entfernung von ca. 60cm, dann kann man die so um die 0,3mm großen Bildpunkte (=Pixel) auf ihm so gerade eben noch erkennen. Ein Pixel entspricht also 2' in Natura. In dem wir dies wieder gleichsetzen: 2' ≡ 1Pixel haben wir für die Vergrößerung V_B am Bildschirm die folgende Beziehung:

V_B=2333Pixel/32' × 2'/1Pixel = 2333/16 = 145,8

Das ist schon ganz ordentlich. Nun können wir mit diesem Wissen die Vergrößerung V_B am Bildschirm auch direkt bestimmen, wenn Teleskopbrennweite f_O und Pixelabstand P_w auf dem Kamerachip bekannt sind:

V_B=2×f_O×tan(120"/2)/P_w

Mit dieser einfachen Beziehung läßt sich für die fokale Projektion die passende Kamera zum Teleskop und umgekehrt wählen. Und falls beides einfach nicht zusammenpassen will, kann man immer noch auf die Okularprojektion bzw. afokale Okularprojektion zurückgreifen.

Auf der Seite Berechnen lassen sich die verschiedenen Möglichkeiten schon mal vorab durchkalkulieren.